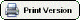example
The following example takes you step by step through an analysis using PERFORM. The following sections are found here.
A. Background
Aluminum lids are produced on a press which has 22 stations. Each day, lids from each station are sampled and the lid height is measured. Each sample contains a single lid from each station. Data are collected over a three-month period. The specifications for this characteristic are 98 ± 5.
B. Loading the Data
The Data have been loaded into a file called example.mvp. This file contains three columns of data. The first column contains the Sample numbers (1-134). The second column contains the Station numbers (1-22). The third column contains the Height measurements. (See Data File Layout.)
From the Main Form menu, select File|Open and load the file example.mvp. The Data Editor will appear as follows. (See Data Editor Overview.)
The variable names are seen at the top of the columns of the Data Grid. From this bottom of this form, it can be seen that there three columns and 2948 rows.
Click the 
speed button to return to the Main Form.
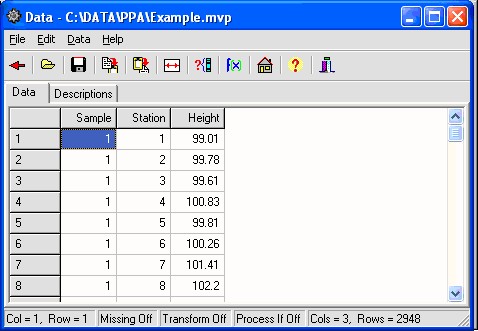
C. Setting-up the Main Form
- Enter a tile into the Title Box as "Lid Height example". (See Main Form.)
- Enter the specifications into the Specification Edit Boxes (98 ± 5 which equates to a USL of 103, a target of 98, and a LSL of 93).
- Select the variable Height, and move it into the Measures box.
- Select the variable Station, and move it into the Grouping Variables box.
The Main Form should appear as follows.
D. Histogram
To view a Histogram of the combined data, click the 
speed button on the Main Form. The following Histogram will be displayed. (See histograms Form.)
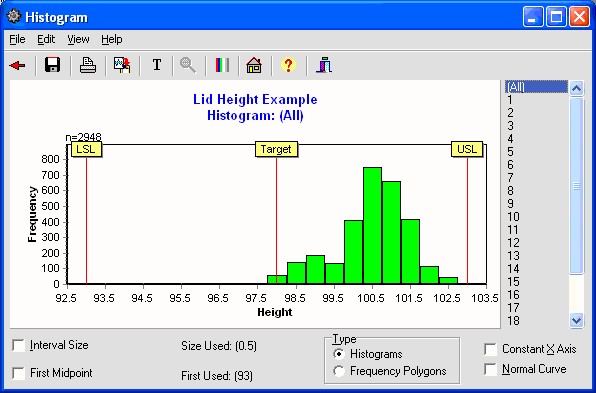
Note the appearance of the Histogram. (See What is a Histogram?)
Click the 
speed button to hide the Histogram and return to the Main Form.
E. Box & Whisker Plots
To view Box & Whisker Plots by Station, Click the 
speed button on the Main Form. The following Box & Whisker Plot will be displayed. (See Box & Whisker Plots Form.)
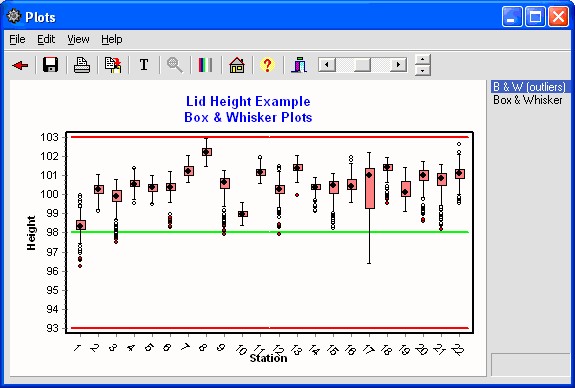
Click on the B&W(Outliers) to see the Box & Whisker Plots with outliers. (See What are Box & Whisker Plots?)
Click the speed button hide the Box & Whisker Plots and return to the Main Form.
F. Control-Charts
For individual observations per process stream, as in this case, you will want to display the charts using X-Charts by Station. Click the 
speed button on the Main Form. In the Variables Control Chart Setup Form, use the following setup. (See What are Control Charts?)
The following X and Moving Range Chart form will be displayed. (See Variables Control Chart Form.)
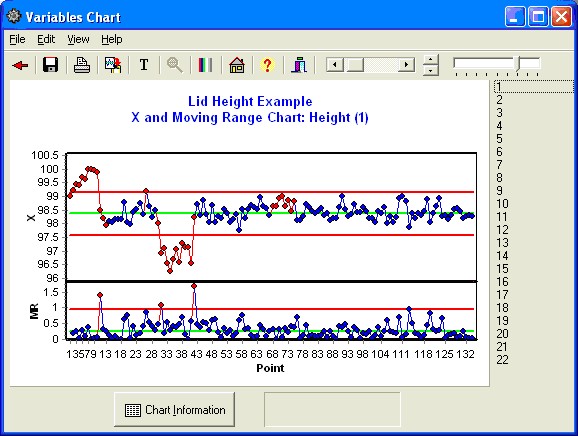
Select the numbers on the right side of the Chart to see X-Charts for each Station.
You may also wish to see the stations combined together. This can be done using a Mean and Standard Deviations Chart (X-bar and s chart). We will do this by selecting "sample" as the sample variable. Within each sample are multiple stations, so we cannot use typical control limits calculations. We will create limits using the Moving Range of the means and standard deviations. Set this up as follows.
You will then see the following chart displayed.
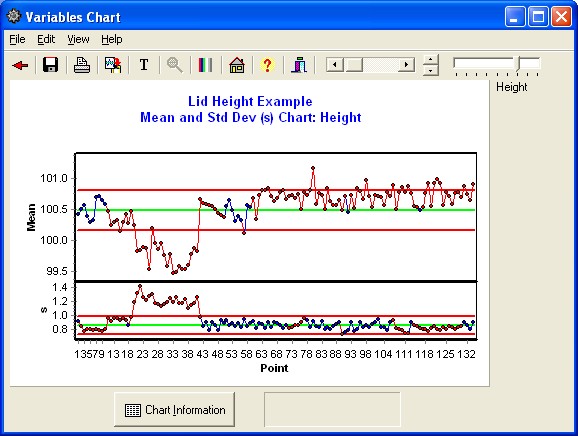
G. Run-Charts
Run charts are simply through-time plots of data without control limits. In this example, we will want to see the Run chart with the specifications.
First set up the chart using the folowing on the Variables Control Chart Setup Form.
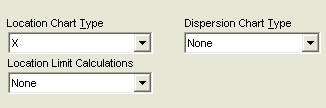
Next, select "Show Specifications" from the View Menu on the Variables Chart Form.
The Control Chart form will now display Run charts using the Specification limits.
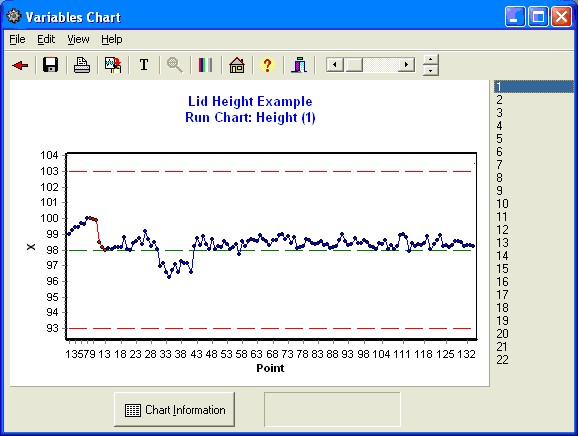
Select the numbers on the right side of the Chart to see Run Charts for each Station compared against the specifications and target.
H. All Data Points Chart
In this output, we want to see all data points from the 22 stations on one chart. Set up the Control chart in the following manner.
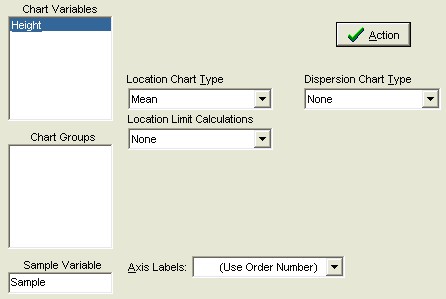
Next from the View Menu select the following Options. (Show All Points, Show Specifications, and Remove Plot of Location Statistics.)
Your chart will now appear as follows. This chart is useful to see the distribution moving through time.
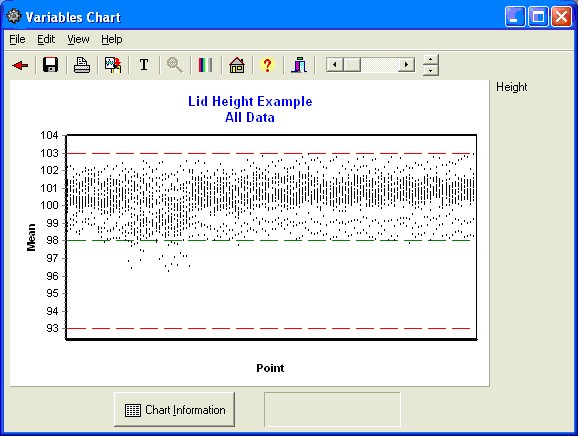
I. Graphics Discussion
The graphical analysis suggests an off-target condition is clearly present as seen in the histogram. The box plots also show significant differences between stations.
The combined data run chart gives a sense of the data through time. A slight change occurred one-fourth of the way through the period, but then stabilized into a consistent pattern.
The X-Charts suggest that the individual stations are not stable through time. When compared against the specification ranges, though, the through-time variation observed appears to be minimal.
J. Performance Analysis
Click the 
button on the Main Form. This will process the data and generate the Process Performance Analysis.
The Text Output Form will be displayed as follows. (See Text Output Form.)
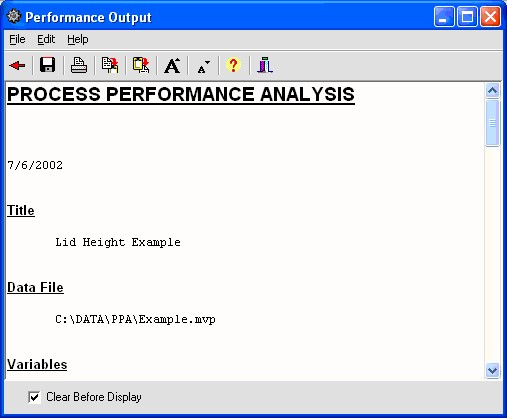
Here is the text output.
PROCESS PERFORMANCE ANALYSIS
1/20/2007
Title
Lid Height example
Data File
C:\Program Files\MVP Programs\Perform\example.mvp
Variables
Measures: Height Groups: Station 1 to 22
Specifications
USL = 103.0000 Target = 98.0000 LSL = 93.0000
Process Stream Analysis
Group n Mean Low High Range Std Std(MMR)
1 134 98.3680 96.2600 99.9800 3.7200 0.6277 0.2621
2 134 100.2191 99.1500 101.0800 1.9300 0.4049 0.2411
3 134 99.7260 97.4800 100.7900 3.3100 0.7662 0.2621
4 134 100.5613 99.5500 101.3900 1.8400 0.2877 0.2201
5 134 100.3560 99.5000 100.9900 1.4900 0.2942 0.2306
6 134 100.2869 98.2900 101.2100 2.9200 0.5854 0.2411
7 134 101.2243 100.6300 102.0600 1.4300 0.3257 0.2411
8 134 102.2103 101.5000 102.9400 1.4400 0.3178 0.2621
9 134 100.3425 97.9300 101.2600 3.3300 0.7890 0.1782
10 134 98.9664 98.3800 99.5800 1.2000 0.2402 0.1468
11 134 101.1778 100.6100 101.9400 1.3300 0.2578 0.2096
12 134 100.1609 97.9300 101.4800 3.5500 0.6743 0.2516
13 134 101.3817 99.9400 102.0600 2.1200 0.2798 0.2411
14 134 100.3308 99.1500 100.9300 1.7800 0.3427 0.2306
15 134 100.2666 98.2600 101.1400 2.8800 0.6785 0.2306
16 134 100.5613 99.5900 101.9400 2.3500 0.4530 0.1887
17 134 100.4739 96.4100 102.2000 5.7900 1.2723 0.2306
18 134 101.3035 99.5500 101.9600 2.4100 0.4947 0.2201
19 134 100.2491 99.1500 101.4300 2.2800 0.5375 0.2096
20 134 100.7978 98.6100 101.7600 3.1500 0.7122 0.2411
21 134 100.5726 98.1900 101.6100 3.4200 0.7952 0.2725
22 134 101.0587 99.5300 102.6300 3.1000 0.4902 0.2725
SQRT(MSW) = Avg Std Dev within = 0.5823
AVG Std(MMR) = Avg Std Dev from Median Moving Range = 0.2311
Descriptives
n = 2948 Mean = 100.4816 Std. Dev = 0.9788 Low = 96.2600 Q1 = 100.0625 Median = 100.5900 Q3 = 101.1400 High = 102.9400 Skewness = -0.732 Kurtosis = 0.759
Variance Components
Total Variance About Target = 7.1165 100.00% Off-target Variance = 6.1584 86.54% Potential Variance = 0.0534 0.75% Process Stream Variance = 0.6190 8.70% Time(Control) Variance = 0.2856 4.01%
Performance
%Off-Target = 24.82% Max Stream Mean = 102.2103 Min Stream Mean = 98.3680 %Process Stream Difference = 38.42% ppk = 0.858 ppm = 0.625 pp = 1.703 pp(Stream)= 2.862 Cp(pot) = 7.212 n = 2948 Above USL = 0 Below LSL = 0 Total Out = 0 (0 ppm)
Click the speed button return to the Main Form.
K. Performance Text Output Discussion
For each of the 22 stations, descriptive statistics are generated including the mean, standard deviation, low, high, and range. In addition, since individual readings are taken in time order, a standard deviation is generated using the median moving range for each station.
The performance measure, ppm was 0.625. pp was 1.703. This suggests a large loss in performance because of lack of targeting. In addition, 38.42% of the specification range is taken up by station to station differences. This could also be thought of as a station targeting issue. This can be seen graphically in the histogram and the box plots.
L. Performance Analysis Charts
To view the Performance Analysis Charts, click the 
speed button on the Main Form. The following Performance Analysis Chart Form will be displayed. (See Performance Charts Form.)
Click the Tabs on the Top of this form to view each of the Performance Analysis Charts.
M. Conclusions
From this analysis, it can be seen that the biggest opportunity comes from getting the individual stations on target. While improvement in control will minimize variation, the through-time sources of variability do not represent the largest opportunity. Measurement error analysis is not shown, but from the process potential assessment, measurement error may be considered negligible.
These results are typical of many observed processes. Improvements in targeting and reduction of tool-to-tool or station-to-station differences often represent an important opportunity. While improvement in through-time stability or control does not represent a large improvement opportunity in this case, it may be critical in others.
