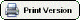ppm
ppm - Assessing Overall Performance
Taguchi defined a loss function which quantifies the losses due to manufacturing variation. As product characteristics depart from their design target, this loss function states that the loss will be proportional to the target deviation squared. Chan, Cheng, and Spiring created a capability measure, Cpm which is inversely related to this loss.
ppm, is derived from Cpm and is inversely related to the losses in a manufacturing process. The higher the ppm value, the better the process performance. When a target, upper, and lower specification are given, ppm is calculated by
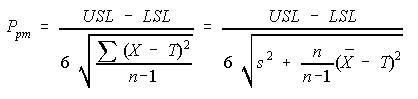
where
- USL is the Upper Specification Limit,
- LSL is the Lower Specification Limit,
- X is the observed value,
- T is the Target,
- s is the sample standard deviation from all combined data,
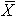 is the sample mean from all combined data, and
is the sample mean from all combined data, and- n is the total number of observations.
Note
When a characteristic is bounded, by zero or some other value, and the target is at the bounds, for example zero for flatness, enter a specification at the bounds and use the above formula. Similarly, if analyzing within part variability which is intended to be zero, use a lower specification and target of zero, and an upper specification equal to the specification range.
For a single specification and target the following is used
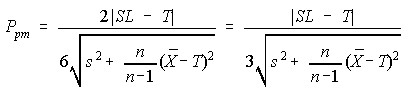
where SL is the Specification Limit.
The use of ppm assumes valid specifications and targets are given and representative samples are generated during the period of interest.
When appropriately employed, ppm may be used as a primary measure to assess the performance of a process. Process performance will improve, as measured by increases in ppm, as:
- the process is brought into better control;
- systematic variation such as differences in tooling, setup, operators, machines, and materials is reduced;
- the process is brought on target; and
- the inherent variation of the process is reduced.