Shapiro-Wilk Exponential Test

The Shapiro-Wilk Test for Exponentiality, with origin parameter unknown, employes the following statistic:

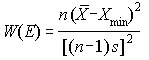
WE-Calc

Where

s is the sample standard deviation,
Xmin is the minimum value in the data set, and
n is the sample size.

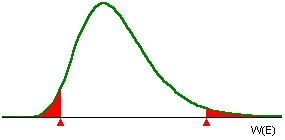
Use the table below to find the critical values for the Shapiro-Wilk Test for Exponentiality. Two critical values are required. Accept the hypothesis that the distribution can be modeled with an Exponential Distribution if test statistic W(E) falls within the two values.

Note that the critical values are single-tailed values, use alpha/2 and (1-alpha)/2 to obtain the appropriate critical values since this is a two-sided test. For example, with alpha = 0.05, select the critical values corresponding to 0.025 and 0.975.

Critical Values For W(E) Test Statistics For Exponentiality

WE-Dist

n	0.005	0.010	0.025	0.050	0.100	0.500	0.900	0.950	0.975	0.990	0.995
	Alpha (single-tailed values)
3	0.2519	0.2538	0.2596	0.2697	0.2915	0.5714	0.9709	0.9926	0.9981	0.9997	0.9999
4	0.1241	0.1302	0.1434	0.1604	0.1891	0.3768	0.7514	0.8581	0.9236	0.9680	0.9837
5	0.0845	0.0905	0.1048	0.1187	0.1442	0.2875	0.5547	0.6682	0.7590	0.8600	0.9192
6	0.0610	0.0665	0.0802	0.0956	0.1173	0.2276	0.4292	0.5089	0.5842	0.6775	0.7501
7	0.0514	0.0591	0.0700	0.0810	0.0986	0.1874	0.3474	0.4162	0.4852	0.5706	0.6426
8	0.0454	0.0512	0.0614	0.0710	0.0852	0.1625	0.2934	0.3497	0.4033	0.4848	0.5428
9	0.0404	0.0442	0.0537	0.0633	0.0751	0.1415	0.2553	0.3005	0.3454	0.4015	0.4433
10	0.0369	0.0404	0.0487	0.0568	0.0678	0.1225	0.2178	0.2525	0.2879	0.3391	0.3701
11	0.0339	0.0380	0.0447	0.0528	0.0616	0.1112	0.1934	0.2265	0.2619	0.3039	0.3314
12	0.0311	0.0358	0.0410	0.0494	0.0567	0.1009	0.1723	0.2019	0.2364	0.2716	0.2978
13	0.0287	0.0337	0.0382	0.0460	0.0528	0.0925	0.1563	0.1829	0.2113	0.2422	0.2642
14	0.0265	0.0317	0.0362	0.0428	0.0496	0.0847	0.1417	0.1647	0.1862	0.2131	0.2315
15	0.0247	0.0298	0.0344	0.0398	0.0466	0.0778	0.1285	0.1485	0.1669	0.1926	0.2123
16	0.0233	0.0280	0.0326	0.0374	0.0438	0.0728	0.1187	0.1355	0.1542	0.1770	0.1931
17	0.0222	0.0264	0.0310	0.0352	0.0412	0.0684	0.1099	0.1257	0.1423	0.1614	0.1794
18	0.0212	0.0250	0.0294	0.0332	0.0388	0.0640	0.1015	0.1164	0.1311	0.1483	0.1668
19	0.0203	0.0238	0.0278	0.0314	0.0368	0.0600	0.0935	0.1071	0.1199	0.1374	0.1452
20	0.0196	0.0227	0.0264	0.0302	0.0353	0.0570	0.0884	0.1002	0.1121	0.1286	0.1369
21	0.0190	0.0217	0.0250	0.0290	0.0337	0.0540	0.0839	0.0948	0.1054	0.1198	0.1288
22	0.0185	0.0208	0.0238	0.0278	0.0323	0.0516	0.0794	0.0894	0.0988	0.1118	0.1212
23	0.0181	0.0201	0.0230	0.0266	0.0310	0.0492	0.0749	0.0836	0.0933	0.1043	0.1142
24	0.0177	0.0194	0.0224	0.0256	0.0298	0.0468	0.0704	0.0788	0.0882	0.0984	0.1071
25	0.0173	0.0188	0.0218	0.0248	0.0286	0.0447	0.0668	0.0749	0.0836	0.0927	0.1000
26	0.0169	0.0182	0.0213	0.0240	0.0274	0.0426	0.0636	0.0712	0.0791	0.0885	0.0948
27	0.0165	0.0177	0.0208	0.0232	0.0264	0.0407	0.0606	0.0678	0.0747	0.0843	0.0896
28	0.0161	0.0172	0.0203	0.0225	0.0256	0.0391	0.0576	0.0649	0.0706	0.0801	0.0859
29	0.0157	0.0168	0.0198	0.0219	0.0249	0.0377	0.0555	0.0621	0.0671	0.0759	0.0822
30	0.0153	0.0164	0.0193	0.0213	0.0242	0.0364	0.0536	0.0593	0.0643	0.0719	0.0786
31	0.0149	0.0160	0.0188	0.0207	0.0235	0.0352	0.0518	0.0569	0.0615	0.0719	0.0753
32	0.0145	0.0156	0.0183	0.0201	0.0229	0.0340	0.0491	0.0547	0.0591	0.0686	0.0722
33	0.0141	0.0152	0.0178	0.0195	0.0223	0.0329	0.0475	0.0527	0.0573	0.0661	0.0691
34	0.0137	0.0148	0.0173	0.0190	0.0217	0.0319	0.0459	0.0507	0.0555	0.0636	0.0660
35	0.0133	0.0144	0.0168	0.0185	0.0211	0.0309	0.0444	0.0488	0.0537	0.0611	0.0639
36	0.0129	0.0141	0.0164	0.0180	0.0205	0.0300	0.0429	0.0470	0.0519	0.0588	0.0608
37	0.0125	0.0138	0.0160	0.0176	0.0200	0.0291	0.0414	0.0454	0.0501	0.0567	0.0578
38	0.0122	0.0135	0.0156	0.0172	0.0195	0.0283	0.0400	0.0440	0.0483	0.0546	0.0553
39	0.0120	0.0133	0.0152	0.0168	0.0190	0.0275	0.0386	0.0426	0.0465	0.0525	0.0531
40	0.0118	0.0131	0.0148	0.0164	0.0186	0.0267	0.0375	0.0414	0.0447	0.0512	0.0510
41	0.0116	0.0129	0.0144	0.0161	0.0182	0.0260	0.0364	0.0402	0.0430	0.0499	0.0493
42	0.0114	0.0127	0.0140	0.0158	0.0178	0.0253	0.0355	0.0389	0.0417	0.0476	0.0482
43	0.0112	0.0125	0.0137	0.0155	0.0174	0.0248	0.0346	0.0379	0.0405	0.0464	0.0471
44	0.0110	0.0123	0.0134	0.0152	0.0170	0.0243	0.0338	0.0369	0.0394	0.0452	0.0460
45	0.0108	0.0121	0.0131	0.0149	0.0166	0.0238	0.0329	0.0359	0.0385	0.0440	0.0449
46	0.0106	0.0119	0.0129	0.0146	0.0162	0.0233	0.0320	0.0349	0.0376	0.0423	0.0438
47	0.0104	0.0117	0.0127	0.0143	0.0158	0.0228	0.0311	0.0340	0.0367	0.0416	0.0427
48	0.0103	0.0115	0.0125	0.0143	0.0158	0.0228	0.0311	0.0340	0.0367	0.0394	0.0426
49	0.0102	0.0113	0.0123	0.0141	0.0155	0.0223	0.0303	0.0332	0.0358	0.0382	0.0416
50	0.0101	0.0111	0.0122	0.0137	0.0149	0.0213	0.0288	0.0317	0.0340	0.0360	0.0394
51	0.0100	0.0109	0.0120	0.0135	0.0147	0.0209	0.0282	0.0310	0.0331	0.0349	0.0383
52	0.0099	0.0107	0.0119	0.0133	0.0145	0.0205	0.0276	0.0303	0.0323	0.0341	0.0373
53	0.0097	0.0106	0.0118	0.0131	0.0143	0.0201	0.0270	0.0296	0.0315	0.0332	0.0363
54	0.0095	0.0104	0.0116	0.0129	0.0141	0.0197	0.0264	0.0289	0.0307	0.0329	0.0353
55	0.0094	0.0103	0.0115	0.0127	0.0139	0.0193	0.0258	0.0282	0.0299	0.0321	0.0343
56	0.0093	0.0102	0.0113	0.0125	0.0137	0.0189	0.0252	0.0275	0.0292	0.0313	0.0333
57	0.0092	0.0101	0.0112	0.0123	0.0135	0.0185	0.0247	0.0268	0.0285	0.0306	0.0324
58	0.0091	0.0100	0.0110	0.0121	0.0133	0.0182	0.0242	0.0262	0.0279	0.0301	0.0318
59	0.0090	0.0098	0.0109	0.0119	0.0131	0.0179	0.0238	0.0257	0.0274	0.0296	0.0312
60	0.0089	0.0095	0.0108	0.0117	0.0129	0.0176	0.0234	0.0252	0.0270	0.0291	0.0306
61	0.0088	0.0093	0.0107	0.0115	0.0127	0.0173	0.0230	0.0247	0.0266	0.0286	0.0301
62	0.0087	0.0092	0.0105	0.0113	0.0125	0.0170	0.0226	0.0242	0.0262	0.0281	0.0296
63	0.0086	0.0091	0.0104	0.0112	0.0123	0.0167	0.0222	0.0238	0.0257	0.0276	0.0291
64	0.0085	0.0090	0.0102	0.0111	0.0121	0.0164	0.0218	0.0234	0.0252	0.0271	0.0286
65	0.0084	0.0089	0.0101	0.0109	0.0119	0.0161	0.0215	0.0230	0.0247	0.0266	0.0281
66	0.0082	0.0088	0.0099	0.0108	0.0117	0.0159	0.0211	0.0225	0.0242	0.0261	0.0276
67	0.0081	0.0087	0.0098	0.0107	0.0115	0.0157	0.0207	0.0221	0.0237	0.0256	0.0271
68	0.0080	0.0086	0.0096	0.0105	0.0114	0.0155	0.0204	0.0217	0.0232	0.0251	0.0266
69	0.0079	0.0085	0.0095	0.0104	0.0113	0.0152	0.0198	0.0213	0.0227	0.0246	0.0261
70	0.0078	0.0084	0.0094	0.0103	0.0111	0.0150	0.0194	0.0209	0.0222	0.0241	0.0256
71	0.0077	0.0083	0.0093	0.0102	0.0109	0.0147	0.0191	0.0205	0.0218	0.0237	0.0251
72	0.0076	0.0082	0.0092	0.0101	0.0108	0.0145	0.0188	0.0201	0.0214	0.0232	0.0246
73	0.0075	0.0081	0.0091	0.0100	0.0107	0.0143	0.0185	0.0198	0.0211	0.0228	0.0241
74	0.0074	0.0080	0.0090	0.0098	0.0106	0.0141	0.0182	0.0195	0.0208	0.0224	0.0236
75	0.0073	0.0079	0.0089	0.0097	0.0105	0.0139	0.0179	0.0192	0.0205	0.0220	0.0231
76	0.0073	0.0078	0.0088	0.0096	0.0104	0.0137	0.0176	0.0189	0.0202	0.0217	0.0227
77	0.0072	0.0077	0.0087	0.0095	0.0103	0.0135	0.0173	0.0186	0.0199	0.0214	0.0223
78	0.0071	0.0077	0.0086	0.0093	0.0101	0.0134	0.0170	0.0183	0.0196	0.0211	0.0219
79	0.0070	0.0076	0.0085	0.0092	0.0100	0.0132	0.0168	0.0180	0.0193	0.0208	0.0215
80	0.0070	0.0075	0.0084	0.0091	0.0099	0.0131	0.0166	0.0177	0.0190	0.0205	0.0211
81	0.0069	0.0074	0.0083	0.0090	0.0098	0.0129	0.0164	0.0175	0.0187	0.0202	0.0207
82	0.0068	0.0074	0.0082	0.0088	0.0097	0.0128	0.0162	0.0173	0.0184	0.0199	0.0203
83	0.0067	0.0073	0.0081	0.0087	0.0096	0.0126	0.0160	0.0170	0.0181	0.0196	0.0199
84	0.0067	0.0073	0.0080	0.0086	0.0095	0.0125	0.0158	0.0168	0.0178	0.0193	0.0196
85	0.0065	0.0072	0.0079	0.0085	0.0094	0.0123	0.0156	0.0166	0.0174	0.0190	0.0193
86	0.0066	0.0071	0.0078	0.0085	0.0093	0.0122	0.0154	0.0164	0.0172	0.0187	0.0190
87	0.0065	0.0071	0.0077	0.0084	0.0092	0.0120	0.0152	0.0162	0.0170	0.0184	0.0187
88	0.0065	0.0070	0.0077	0.0084	0.0091	0.0119	0.0150	0.0160	0.0168	0.0181	0.0185
89	0.0064	0.0070	0.0076	0.0083	0.0090	0.0117	0.0148	0.0158	0.0166	0.0179	0.0183
90	0.0064	0.0069	0.0075	0.0082	0.0089	0.0116	0.0147	0.0156	0.0164	0.0176	0.0181
91	0.0063	0.0068	0.0075	0.0082	0.0088	0.0114	0.0145	0.0154	0.0162	0.0173	0.0179
92	0.0063	0.0068	0.0074	0.0081	0.0087	0.0113	0.0143	0.0153	0.0160	0.0171	0.0177
93	0.0062	0.0067	0.0073	0.0081	0.0086	0.0112	0.0141	0.0151	0.0158	0.0168	0.0175
94	0.0062	0.0067	0.0073	0.0080	0.0085	0.0110	0.0139	0.0149	0.0156	0.0165	0.0173
95	0.0061	0.0066	0.0072	0.0079	0.0084	0.0109	0.0138	0.0147	0.0154	0.0163	0.0171
96	0.0061	0.0065	0.0072	0.0078	0.0083	0.0108	0.0136	0.0145	0.0153	0.0161	0.0169
97	0.0060	0.0065	0.0071	0.0077	0.0082	0.0107	0.0134	0.0143	0.0152	0.0159	0.0167
98	0.0060	0.0064	0.0070	0.0076	0.0081	0.0105	0.0133	0.0142	0.0151	0.0157	0.0165
99	0.0059	0.0064	0.0070	0.0075	0.0080	0.0104	0.0132	0.0140	0.0150	0.0155	0.0163
100	0.0059	0.0063	0.0069	0.0074	0.0079	0.0103	0.0131	0.0139	0.0149	0.0153	0.0161