A Poisson Distribution is a discrete Random Sampling Distribution. The sampling is from a given unit of inspection or observation. These units of observation can be properties such as length, area, number of items, volume, or time. The Poisson distribution is generated by counts of the number of occurrences of some phenomenon.
Calculations
The probability of exactly X occurrences in unit of observation may be calculated by the following Poisson formula.
![]()
Where:
- X is the number of occurrences, and
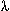 is the mean number of occurrences.
is the mean number of occurrences.
Other Properties
The poisson distribution may be approximated with a Normal Distribution with a Mean equal to ![]() , and a standard deviation equal to the square-root of
, and a standard deviation equal to the square-root of ![]() .
.
The limit of the Binomial Distribution, as n goes toward infinity, and p goes toward zero, yields a Poisson Distribution, with ![]() equal to np.
equal to np.
The distance or time between occurrence of Poisson phenomenon can be model with an Exponential distribution.
example
Here is an example Poisson Distribution, with a mean number of occurrences, ![]() , equal to 2. The probability of 3 or more occurrences, when
, equal to 2. The probability of 3 or more occurrences, when ![]() is 2, is 0.3233.
is 2, is 0.3233.
Poisson Distribution
Lambda = 2.0000
Prob Equal & Equal &
X at X Above Below
0 0.1353 1.0000 0.1353 |------------------
1 0.2707 0.8647 0.4060 |-----------------------------------
2 0.2707 0.5940 0.6767 |-----------------------------------
3 0.1804 0.3233 0.8571 |-----------------------
4 0.0902 0.1429 0.9473 |------------
5 0.0361 0.0527 0.9834 |-----
6 0.0120 0.0166 0.9955 |--
7 0.0034 0.0045 0.9989 |
8 0.0009 0.0011 0.9998 |
9 0.0002 0.0002 1.0000 |
10 0.0000 0.0000 1.0000 |
11 0.0000 0.0000 1.0000 |
12 0.0000 0.0000 1.0000 |
13 0.0000 0.0000 1.0000 |
14 0.0000 0.0000 1.0000 |
15 0.0000 0.0000 1.0000 |
\ \ \ \
Inf. 0.0000 0.0000 1.0000 |