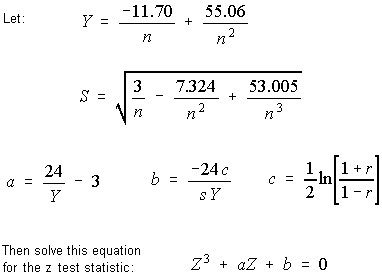The Lin-Mudholkar test is based on the fact that the mean and variance of a random sample are independently distributed, if and only if, the parent population is normal (Lin and Mudholkar, 1980).
The test is sensitive only to departures from normality due to skewness. As shown by Lin and Mudholkar (1980), the procedure is generally much more powerful at detecting skewness than is the coefficient of Skewness.
The procedure has little power in detecting non-normal symmetrical distributions. For example, uniform or platykurtic distributions will pass this test easily. Therefore, other tests, such as Anderson-Darling, should also be consulted if there is a concern for this type of departure from normality.
A minimum sample size of 10 is recommended for this procedure.
Procedure
- Start with a column of data.
- For each value in the data set, temporarily drop the value and calculate a new mean and variance with the remaining data. Replace the value and repeat the procedure with each of the remaining values in the data set. Place the new means and variances in two new columns. Then take the cube root of each variance (a transformation to normalize). You will now have two new columns, one containing means, and the other containing cube-roots of variances.
- Calculate the Pearson Product Moment Correlation coefficient, r, between the generated means and cubed root of the variances.
- To determine significance, solve the following equations. The Z value is a standard z score, from which the two-tailed probabilities will yield the significance.