<< Return  Print

The Two-Sample Independent Tests are used to test if differences exist in means and dispersion of two independent populations from which the samples were drawn. Several tests are performed.

Three methods may be used to test for differences in population means: when the standard deviations are known, when the standard deviations are unknown but assumed equal, and when the standard deviations are unknown and assumed not equal.

Three separate tests are conducted to test for differences in dispersion. The first, the F-test, tests for differences in variances. The second, the Levene test, tests for differences in absolute deviations from the mean (MAD). The third, the ADM(n-1), tests for differences in absolute deviations about the median, dropping one point at the median from each sample. The Levene and ADM(n-1) tests are available only if data is read from a file.

Hypotheses

The following hypotheses may be tested:

Means

Where and are the population means from which the samples were drawn.

Dispersion

Where and are the population variances from which the samples were drawn.

Assumptions (Means)

1. The samples have been randomly drawn from two independent populations (Critical)
2. The population from which the sample has been drawn is normally distributed (Not Critical)
3. The standard deviation is known, or unknown (Critical for small samples sizes)
4. The measurements are at least Interval Level (Critical)

Assumptions (Dispersion)

1. The samples have been randomly drawn from two independent populations (Critical)
2. The population from which the sample has been drawn is normally distributed (Critical for F-test, generally critical for Levene, and the ADM(n-1) is robust to this assumption.)
3. The measurements are at least Interval Level (Critical)

Test Statistics (Means)

Independent Two-Sample Test for Differences in Means

Standard Deviations are Known

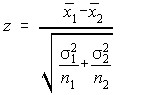
Standard Deviations Unknown, but Assumed Equal

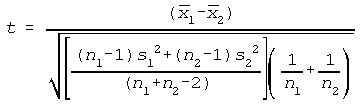
Where t has n1 + n2 - 2 df

Standard Deviations Unknown, and Assumed Unequal

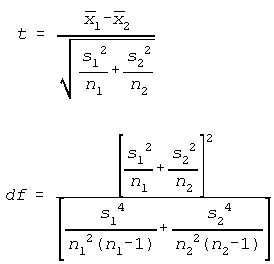
Test Statistics (Dispersion)

F-Test

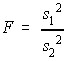
Where F has (n1 - 1, n2 - 1) df

Levene Test

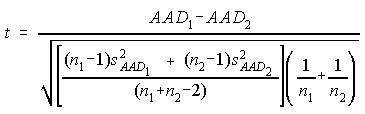
Where AAD is the average absolute deviation about the sample means,

and t has n1 + n2 - 2 df

ADM(n-1) Test

Where ADM is the average absolute deviation about the sample medians with a center point from each sample dropped from the analysis. If the sample size is odd, the median point is dropped (a zero absolute deviation), if the sample size is even, one of the two middle values are dropped. t has n1 + n2 - 4 df

Output

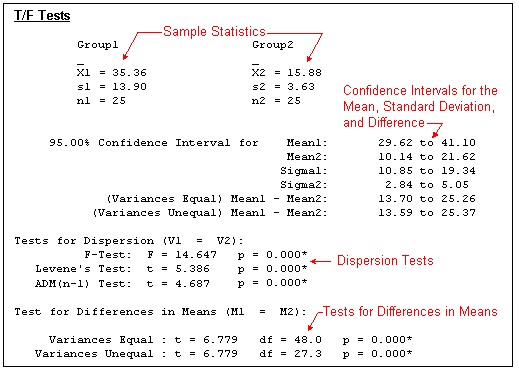
Note

The p-value is flagged with an asterisk (*) when p <= alpha.