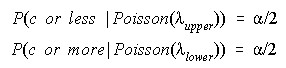What are Confidence Intervals?
Sample statistics, such as sample means, proportions,and standard deviations, may be used to estimate the population parameters from which the sample was drawn. These estimates will probably not exactly equal the true population parameters. The difference between the true value and the sample value is caused by sampling error.
Confidence intervals provide a range of values in which we would expect to find the true population parameter, with a given level of confidence. A 95% confidence interval for a population mean is the interval that has a 95% chance of the true population mean being found within it. An interval estimate provides us a way to qualify our estimate by indicating the magnitude of the sampling error, and hence, the precision of our estimate.
Winer (1971, p10) says, "The procedure by which the upper and lower confidence bounds are determined will, in the long run (if the study is repeated many times), ensure that the proportion of correct statements is equal to the level of confidence for that interval." To find this interval, we must look at the set of all possible parameters and assess each of those parameters for their probability of providing us with the sample statistic we observed.
Statisticians have created formulas for the generation of various confidence intervals. Below are the formulas used by MVPstats to generate these intervals.
Confidence Interval Calculations
Means (Sigma Known)
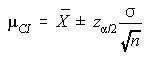
Means (Sigma Unknown)
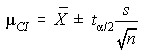
Difference in Means (Independent Samples, Sigmas Known)
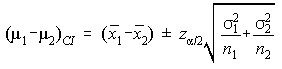
Difference in Means (Independent Samples, Sigma Unknown, Variances Equal)
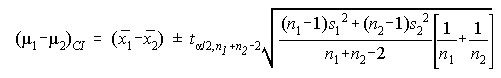
Difference in Means (Independent Samples, Sigma Unknown, Variances Unequal)
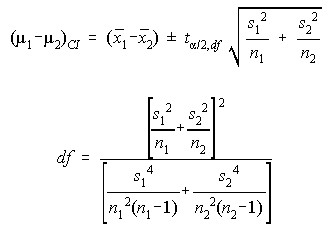
Difference in Means (Dependent Samples)
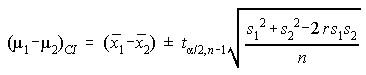
Standard Deviation
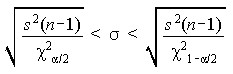
Correlation
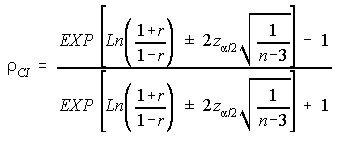
Proportion (Exact Binomial)
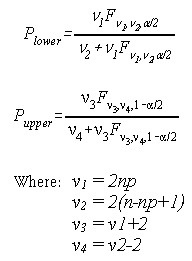
Poisson Rate (Exact Poisson)