A hypergeometric distribution is a discrete random sampling distribution. The sampling is from a series of n trials, from a finite population of size N. Each trial may have outcomes which fall into one of two classifications.
Calculations
The probability of exactly r occurrences in n trails may be calculated by the following hypergeometric formula.
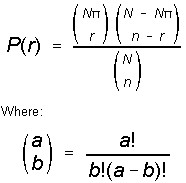
- r is the number of occurrences,
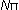is the number of occurrences in the Population,- N is the Population size, and
- n is the sample size.
Other Properties
The limit of the hypergeometric distribution, as the ration of n/N goes toward zero, yields a Binomial Distribution.
example
Here is an example hypergeometric distribution, assuming a sample size of 10, a population of size 100, and a probability of occurrence of 0.15. The probability of observing no occurrences with a sample of size 10 from a population of size 100, with a probability of 0.15 is 0.1808.
Hypergeometric Distribution
p = 0.1500 n = 10 N = 100
np = 1.5000 Np = 15.0000
Prob Equal & Equal &
r at r Above Below
0 0.1808 1.0000 0.1808 |------------------
1 0.3568 0.8192 0.5375 |-----------------------------------
2 0.2919 0.4625 0.8295 |-----------------------------
3 0.1297 0.1705 0.9592 |-------------
4 0.0345 0.0408 0.9937 |---
5 0.0057 0.0063 0.9994 |-
6 0.0006 0.0006 1.0000 |
7 0.0000 0.0000 1.0000 |
8 0.0000 0.0000 1.0000 |
9 0.0000 0.0000 1.0000 |
10 0.0000 0.0000 1.0000 |