Hotelling's Two-Sample Dependent Test for Correlation is used to test if differences exist in correlations from two dependent bivariate populations from which the samples were drawn.
Hypotheses
The following hypotheses may be tested:
Where 
and 
are the population correlations from which the samples were drawn.
Assumptions
1. The samples has been randomly drawn from two dependent bivariate (two-dimensional) populations (Critical)
2. The populations may be modeled with a bivariate normal distribution (Not Critical, if unimodal)
3. The correlations represent the degree to which a linear relationship exists between two variables (Critical)
Test Statistics
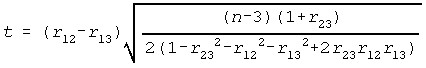
Where t has n-3 df.
Output
Note: The p-value is flagged with an asterisk (*) when p <= alpha.