The Shapiro-Wilk test for normality is a very powerful test. This test is a regression-type test. It assesses how well the observed cumulative frequency distribution curve fits the expected cumulative frequency curve. The Shapiro-Wilk test is sensitive to both skewness and kurtosis. The Shapiro-Wilk and Anderson-Darling tests are comparable in power, with Shapiro-Wilk having a slight edge in many situations.
Procedure
Order the observations from low to high.
- Compute
S² = (n-1)s²
where s² is the sample variance.
- If n is even, k = n/2. If n is odd, k = (n – 1)/2. Then
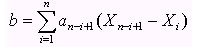
where a(n+i+1) for i = 1 to k, are found in tables.
- Compute the test statistic.
W = b²/S²
- A p-value is generated to evaluate the significance of W.
The algorithms used by MVPstats are those of Patrick Royston, Applied Statistics, vol. 44 no. 4 (1995).
Accurracy is claimed for samples size from 3 to 5000. Sample size less than three will not produce a Shapiro-Wilk statistic.