Mean/Dispersion Two-Sample Dependent Tests
The Two-Sample Dependent Tests are used to test if differences exist in means and dispersion of two dependent populations from which the samples were drawn. The sampling methods may be repeated measures or matched pairs.
Three tests are employed to compare dependent populations. The first is the One-Sample Test for Correlation, the second is the Matched-Pairs t-test for Variance, and the third is the Paired t-test for differences in the Mean.
Hypotheses
The following hypotheses may be tested:
Correlation
![]()
Means
![]()
Where ![]() and
and ![]() are the population means from which the samples were drawn.
are the population means from which the samples were drawn.
The first hypothesis set could also be written as:
![]()
Where ![]() is the average paired difference.
is the average paired difference.
Dispersion
![]()
Where ![]() and
and ![]() are the population variances from which the samples were drawn.
are the population variances from which the samples were drawn.
Assumptions
- The samples have been randomly drawn from two dependent populations either through matching or repeated measures (Critical)
- The population of differences from which the sample pairs have been drawn is normally distributed (Not Critical)
- The measurements are at least Interval Level (Critical)
Test Statistics (Means)
Paired-T-test for Differences in Means
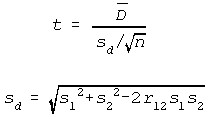
Where:
- D-bar is the average difference in means,
- n is the number of pairs, and
- t has n - 1 df
Test Statistics (Dispersion)
Matched-Pairs t-Test for Variances
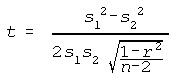
Where t has n - 2 df
Output

Note
The p-value is flagged with an asterisk (*) when p <= alpha.