Proportion Tests Two-Sample
The Two-sample Proportion tests are used to test if the samples were drawn from a populations with equal proportions. Both exact and approximate tests may be performed.
Hypotheses
The following hypotheses may be tested:
![]()
Where ![]() and
and ![]() are the population proportions from which samples were drawn.
are the population proportions from which samples were drawn.
Assumptions
- The samples has been randomly drawn from two independent populations (Critical)
- The populations may be modeled with a binomial distribution, which has these attributes:
- Only two possible outcomes or classifications occur with each item examined (Critical)
- The probability of occurrence of each classification remains fixed from item to item over time (Critical)
- The probability of occurrence of each item sampled is independent of all other items sampled (Critical)
Test Statistics
Approximate Test
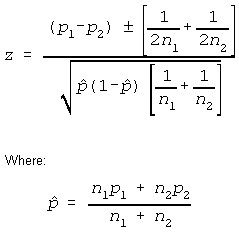
Where the +/- sign is determined as follows for the above hypothesis:
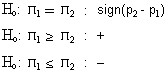
Fisher Exact Test
If we let:
| a = np1 | b = np2 | N = a + b + c + d |
| c = n1(1 - p1) | d = n2(1 - p2) |
Assuming a+b, c+d, a+c, and b+d as fixed, then the probability of obtaining exactly a and b within the sample is:
![]()
This represents the probability of exactly a and b occurrences. These probabilities are calculated for all possible results departing as much or more as a and b. The sum of these probabilities is the one-tailed significance. For two-sided tests the probabilities are calculated for all possible cases where the following is as great or greater than that observed:
![]()
Output

Note
The p-value is flagged with an asterisk (*) when p <= alpha.