The One-sample Mean test is used to test if the sample was drawn from a population with a mean equal to some hypothesized value. Two forms of the test are provided: when the standard deviation is known, and when it is unknown.
Hypotheses
The following hypotheses may be tested:
![]()
Where ![]() is the true population mean from which the sample was drawn, and
is the true population mean from which the sample was drawn, and ![]() is the hypothesized population value.
is the hypothesized population value.
Assumptions
- The sample has been randomly drawn from the population (Critical)
- The population from which the sample has been drawn is normally distributed (Not Critical)
- The standard deviation is known, or unknown (Critical for small samples sizes)
- The measurements are at least Interval Level (Critical)
Test Statistics
Standard Deviation Known
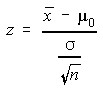
Standard Deviation Unknown
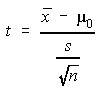
Where t has n -1 df
Output

Note
The p-value is flagged with an asterisk (*) when p <= alpha.